The aim of this activity is to measure physical quantities using video processing. Image processing learned from previous activities can be utilized on image frames of a video. A camera was used to capture a video showing a kinematic phenomenon. We chose to observe a pendulum and obtain the acceleration due to gravity.
For segmentation, the RGB layers for a single frame were observed. It was shown in Figure 1. It can be seen that the bob of the pendulum is more prominent in the green layer. Thus, it can be set to a threshold value to isolate the bob of the pendulum.
 |
| Figure 1. RGB layers of a single frame |
The threshold value that was used was 0.5. Figure 2 shows the segmented image of five consecutive frames. Differences between consecutive frames are not very evident since there is 24.39 frames per second.
 |
| Figure 2. Segmented images of five consecutive frames |
The method for obtaining the period and the acceleration due to gravity was quite unique. One way is to obtain the center of mass of the bob of the pendulum. However, an easier way is to observe the overlapping of consecutive frames. The basic theory in a pendulum was utilized here. As the bob of the pendulum reaches the point of minimum kinetic energy, the distance travelled at a certain time decreases. Since the time interval between each frame is constant, the overlap between two consecutive frames increase. On the other hand, as the bob reaches the point wherein the kinetic energy is at its maximum the distance that the bob has move increases. Thus, the overlap between two consecutive frames is then smaller.
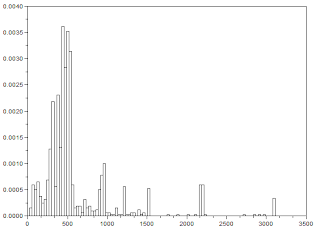
To know the number of pixels that overlaps between consecutive frames, the images were first multiplied. Then the sum of the matrix of their product was obtained. This was done for 100 frames. Figure 3 shows the plot of the number of overlapping pixels vs. frame. It can be seen that there are several peaks.
.PNG) |
| Figure 3. Number of overlapping pixels |
These peaks suggests the relative time at which the bob of the pendulum reaches minimum kinetic energy. Therefore, alternating peaks constitute for the period of the pendulum. Since there are 24.39 frames per second, the period of the pendulum is 1/24.39 which is equal to 0.0410004 sec.
Given the period and the length of the string, the acceleration due to gravity can then be calculated. Note that the length of the string is 30cm. From Figure 3, there are 26 frames that will complete a period. The acceleration due to gravity is given by
Inserting all the obtained value for each parameters, the equation becomes
The calculated acceleration due to gravity was found to be 10.409776m/sec. The analytical value for the acceleration due to gravity is 9.81m/sec. The percent error is then
The obtained percent error is relatively low. Thus, the use of image processing on series of images to calculate physical quantities are also efficient.
Reference
[1] Soriano, M. A12 - Video Processing. 2012
Self - evaluation
I will give myself a grade of 11 for producing the output in a more intuitive and a much easier manner. The calculated physical quantity was indeed near the accepted value. Also, ideas from previous activities were utilized.


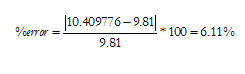









.png)




.PNG)





.png)


.png)



















